弘前データ５：BART による BP 予測

著者

司馬博文

日付

8/11/2025

library(readxl)
library(knitr)
df <- readRDS("df.rds")
library(showtext)
showtext_auto()

備考は全て外し，LOX_Index と 判別式 も説明変数としては考慮しない．

library(dplyr)
df_filtered <- df %>%
  filter(is.na(BP備考), type != "D") %>%
  select(-c(BP備考, LOX_Index, 判別式, id, med_col, 年代)) %>%
  droplevels()

1 CART モデル

1.1 回帰モデル

library(rpart)
library(rpart.plot)

control_params <- rpart.control(maxdepth = 5)

cart_model <- rpart(
  BP ~ .,        # 目的変数を5クラスのものに変更
  data = df_filtered,
  method = "anova",       # 分類なので "class" のまま
  control = control_params
)
printcp(cart_model)


Regression tree:
rpart(formula = BP ~ ., data = df_filtered, method = "anova", 
    control = control_params)

Variables actually used in tree construction:
[1] BMI    FLCΣ   LOX    不安感

Root node error: 81.91/560 = 0.14627

n=560 (4 observations deleted due to missingness)

        CP nsplit rel error xerror    xstd
1 0.055480      0   1.00000 1.0057 0.21310
2 0.031846      1   0.94452 0.9954 0.20224
3 0.028171      2   0.91267 1.1215 0.20807
4 0.019700      3   0.88450 1.1146 0.20688
5 0.011170      4   0.86480 1.1579 0.21068
6 0.010133      6   0.84246 1.1796 0.20804
7 0.010000      8   0.82220 1.1866 0.21100

# 決定木を可視化
rpart.plot(cart_model, 
           type = 4,             # ノードのラベル表示形式
           extra = 101,          # 各ノードにレコードの割合(%)と目的変数の平均値を表示
           under = TRUE,           # 分岐の下に箱を表示
           fallen.leaves = TRUE, # 最終ノード（葉）をグラフの下部に揃える
           box.palette = "auto"  # ノードの色を自動で設定
          )

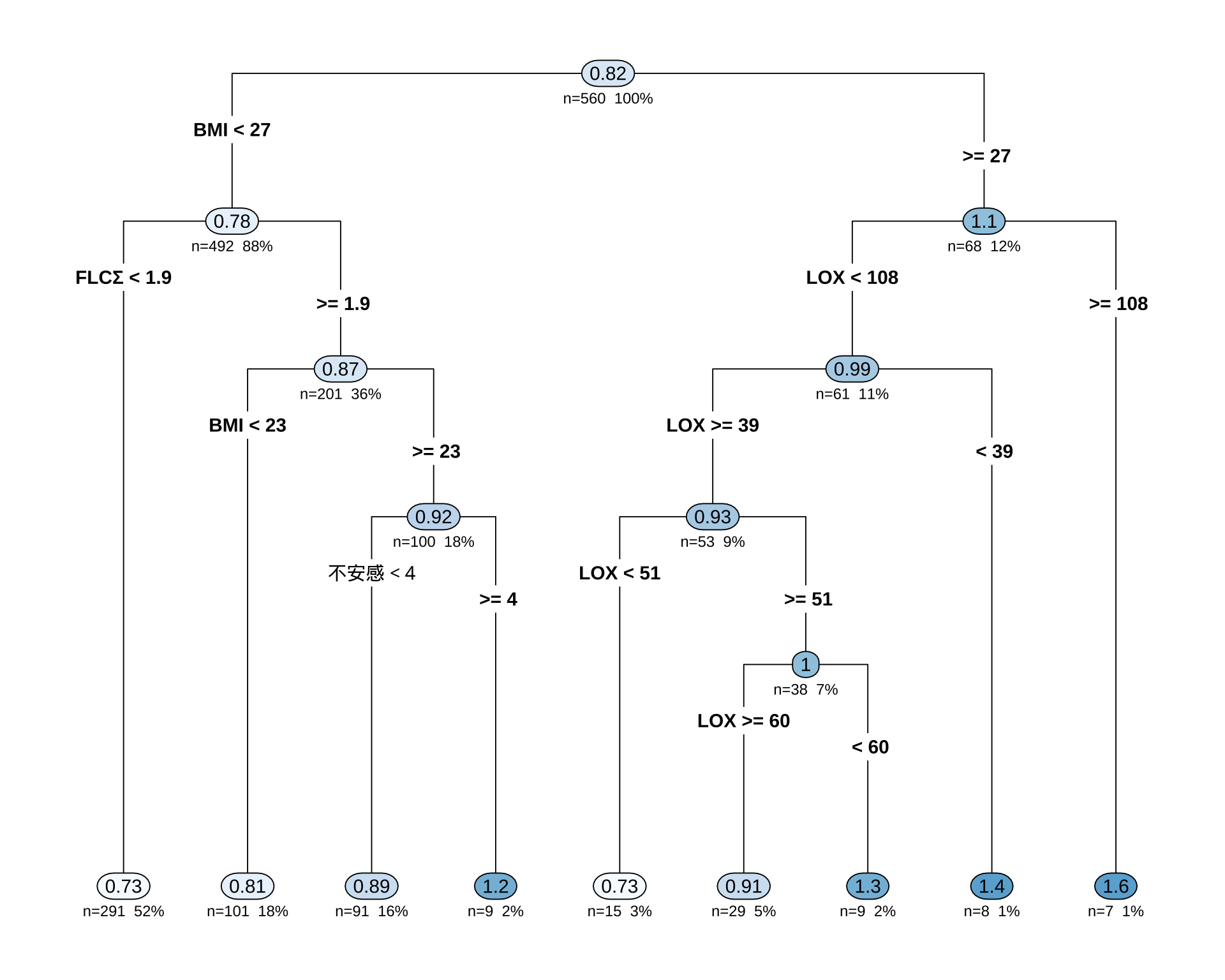
初っ端から「女性ならばほとんど Type B だ」と決めつけているのが面白い．

1.2 モデル評価

# モデルを使って予測値を計算
predictions <- predict(cart_model, newdata = df_filtered)

# 実際値と予測値のデータフレームを作成
results <- data.frame(
  Actual = df_filtered$BP,
  Predicted = predictions
)

# ggplot2を使った可視化例
library(ggplot2)

ggplot(results, aes(x = Predicted, y = Actual)) +
  geom_point(alpha = 0.6) +                               # 点をプロット
  geom_abline(color = "red", linetype = "dashed", size = 1) + # y=xの線を引く
  labs(
    title = "予測値 vs. 実際値 プロット",
    x = "モデルによる予測値 (Predicted)",
    y = "実際の観測値 (Actual)"
  ) +
  theme_minimal()

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.

Warning: Removed 4 rows containing missing values or values outside the scale range
(`geom_point()`).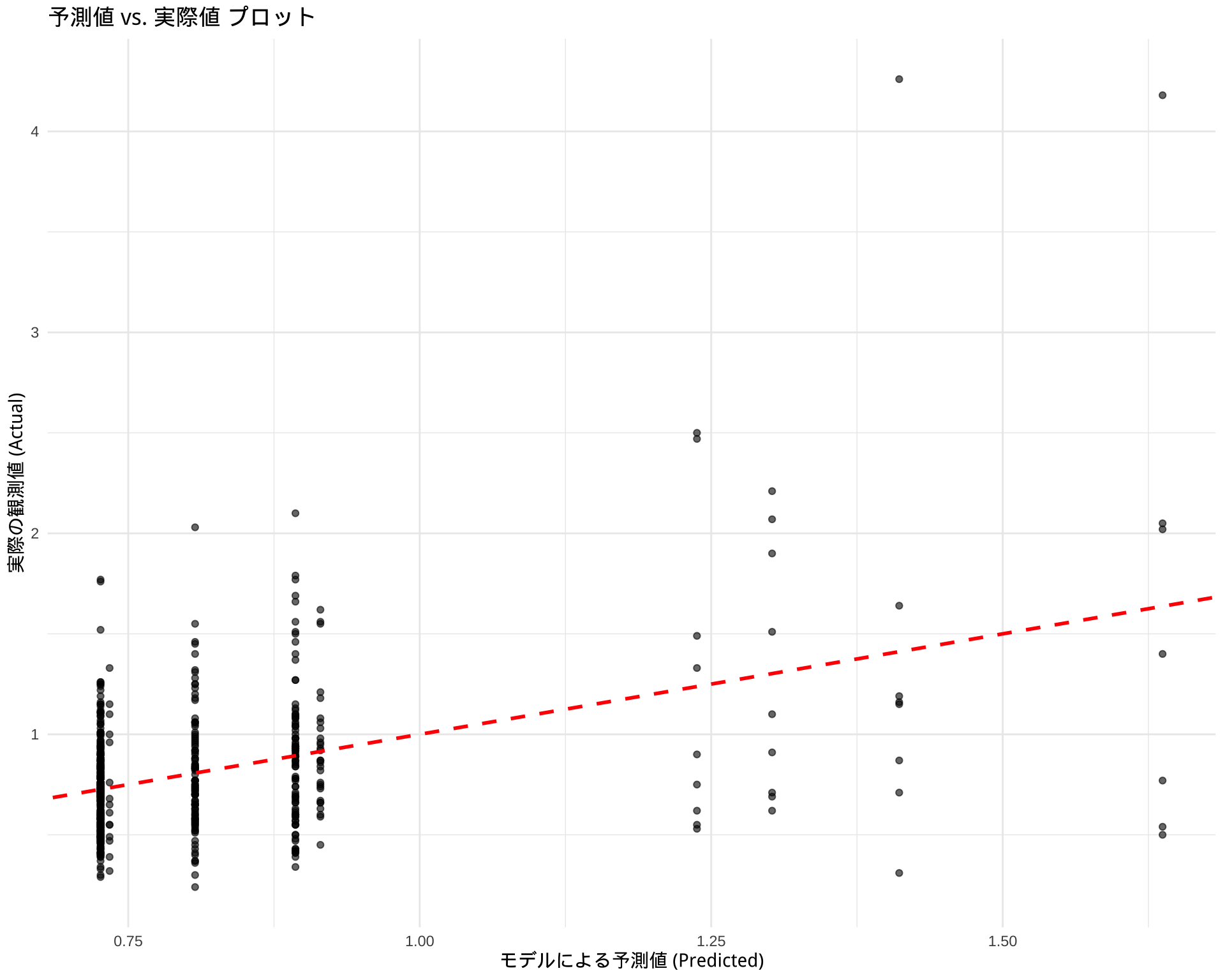

1.3 分類モデル

sum(df$BP > 1.2, na.rm = TRUE) / sum(!is.na(df$BP))

[1] 0.1241071

library(rpart)
library(rpart.plot)

df$BP_flag <- case_when(
  df$BP > 1.2 ~ 2,
  df$BP <= 1.2 ~ 1
) %>%
factor(levels = c(1, 2), labels = c("Normal", "High"))

df_filtered <- df %>%
  filter(is.na(BP備考)) %>%
  select(-c(BP備考, LOX_Index, 判別式, id, med_col, 年代, BP))

# df_filtered からモデルを構築
# BP_level ~ . は、「BP_level を他の全ての変数で説明する」という意味
cart_model <- rpart(
  BP_flag ~ .,
  data = df_filtered,
  method = "class" # 分類問題なので "class" を指定
)

# 結果の要約を表示
printcp(cart_model)


Classification tree:
rpart(formula = BP_flag ~ ., data = df_filtered, method = "class")

Variables actually used in tree construction:
[1] BMI  FLCΣ

Root node error: 54/576 = 0.09375

n=576 (8 observations deleted due to missingness)

        CP nsplit rel error xerror    xstd
1 0.027778      0   1.00000 1.0000 0.12955
2 0.010000      2   0.94444 1.1852 0.13968

# 決定木を可視化
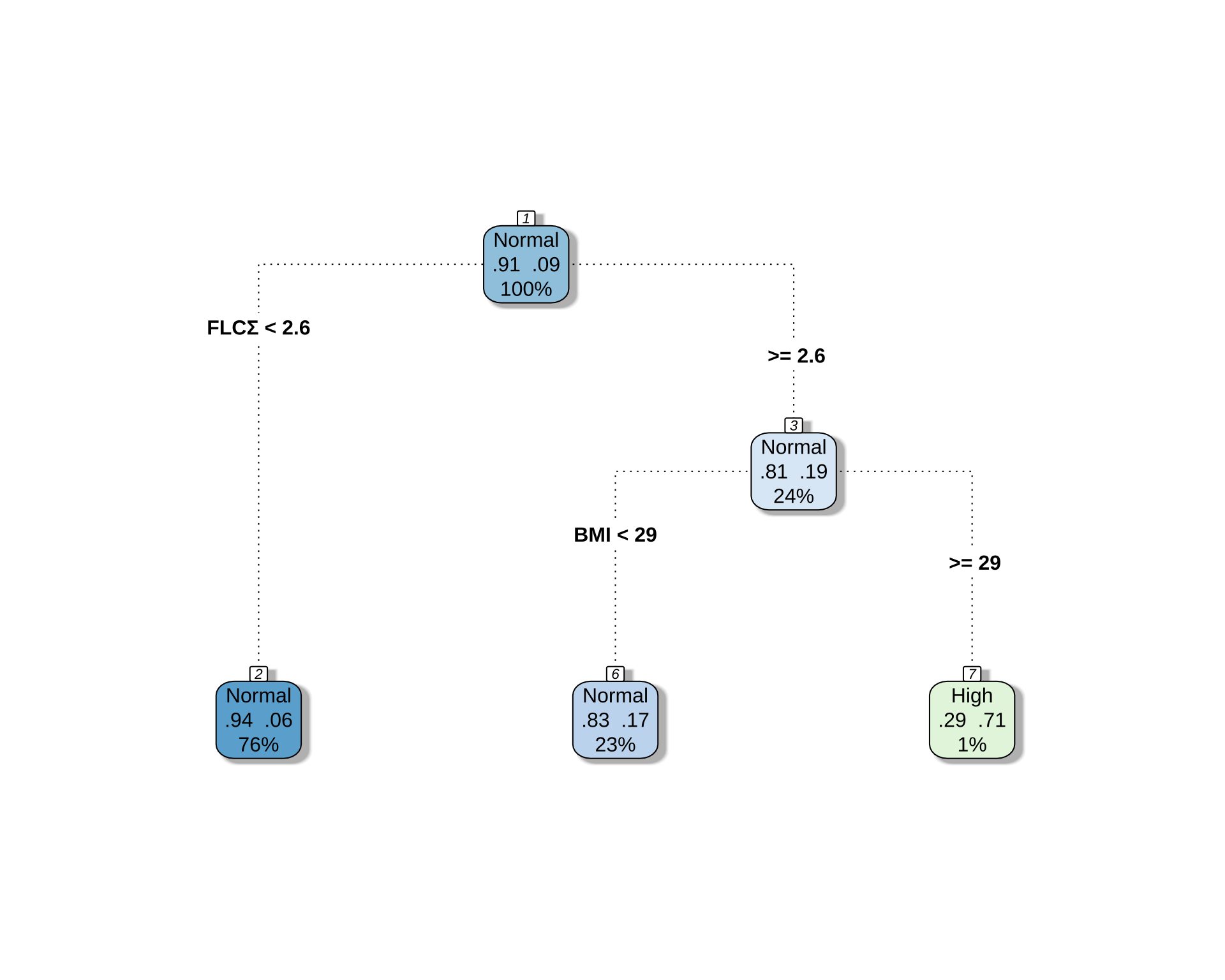
rpart.plot(
  cart_model,
  type = 4,           # ノードの表示スタイル
  extra = 104,        # 各ノードに所属するクラスの割合を表示 (例: L/M/H -> 239/12/0)
  box.palette = "BuGn", # カラーパレット
  branch.lty = 3,     # 枝の線の種類
  shadow.col = "gray", # 影の色
  nn = TRUE           # ノード番号を表示
)

# 予測値を取得
predictions <- predict(cart_model, newdata = df_filtered, type = "class")

# 混同行列を作成
confusion_matrix <- table(Actual = df_filtered$BP_flag, Predicted = predictions)
print(confusion_matrix)

        Predicted
Actual   Normal High
  Normal    520    2
  High       49    5

# 正答率を計算
accuracy <- sum(predictions == df_filtered$BP_flag, na.rm = TRUE) / sum(!is.na(df_filtered$BP_flag))
cat("正答率:", round(accuracy * 100, 2), "%\n")

正答率: 91.15 %

正答率は 90.6% から 91.15% になるだけである．つまり，上位 12 % の BP 者を決定木的に予測することは，与えられた説明変数からはほとんど無理なタスクである．

1.4 3分類モデル

library(dplyr)
df$BP_level <- case_when(
  df$BP > 0.9 ~ 3,
  df$BP > 0.6 & df$BP <= 0.9 ~ 2,
  df$BP <= 0.6 ~ 1
) %>%
factor(levels = c(1, 2, 3), labels = c("<= 0.6", "0.6 ~ 0.9", "> 0.9"))

sum(df$BP > 0.9, na.rm = TRUE) / sum(!is.na(df$BP))

[1] 0.3107143

sum(df$BP > 0.6 & df$BP <= 0.9, na.rm = TRUE) / sum(!is.na(df$BP))

[1] 0.4035714

sum(df$BP <= 0.6, na.rm = TRUE) / sum(!is.na(df$BP))

[1] 0.2857143

library(ggplot2)

ggplot(subset(df, !is.na(BP_level)), aes(x = BP_level, fill = BP_level)) +
  geom_bar(stat = "count", alpha = 0.8) +
  geom_text(data = subset(df, !is.na(BP_level)), aes(label = scales::percent(..count../sum(..count..), accuracy = 0.1)), stat = "count", size = 24) +
  scale_fill_brewer(palette = "Set2") +
  labs(
    title = "BP値の度数分布（3つのbinに分割）",
    x = "BP値の範囲",
    y = "度数",
    fill = "BP値の範囲"
  ) +
  theme_minimal() +
  theme(
    axis.text.x = element_text(size = 15, vjust = 3),
    legend.position = "none",
  )

Warning: The dot-dot notation (`..count..`) was deprecated in ggplot2 3.4.0.
ℹ Please use `after_stat(count)` instead.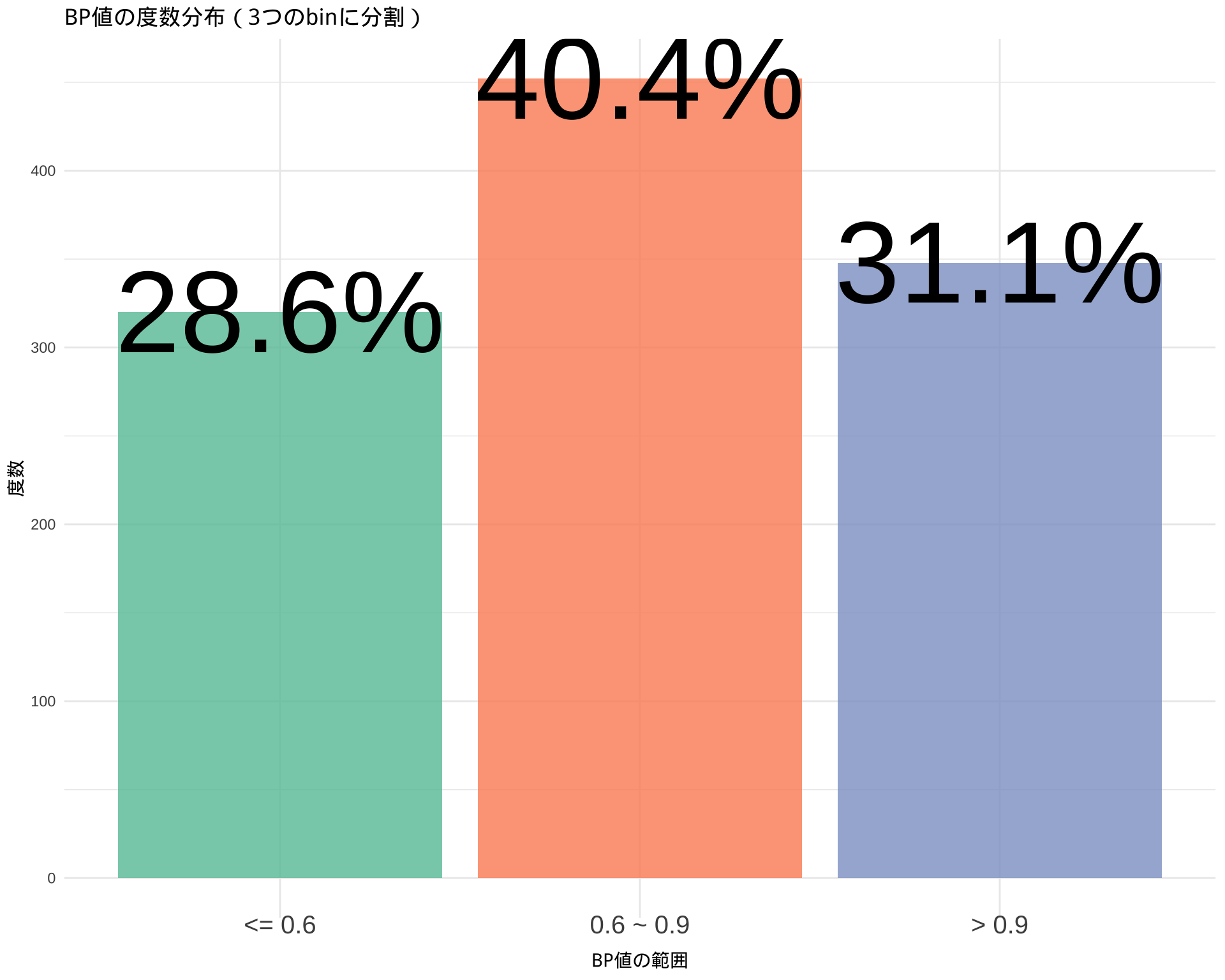

library(rpart)
library(rpart.plot)

df_filtered <- df %>%
  filter(is.na(BP備考)) %>%
  select(-c(BP備考, LOX_Index, 判別式, id, med_col, age, BP, BP_flag))

control_params <- rpart.control(maxdepth = 3)
# BP_level ~ . は、「BP_level を他の全ての変数で説明する」という意味
cart_model <- rpart(
  BP_level ~ .,
  data = df_filtered,
  method = "class", # 分類問題なので "class" を指定
  control = control_params
)

# 結果の要約を表示
printcp(cart_model)


Classification tree:
rpart(formula = BP_level ~ ., data = df_filtered, method = "class", 
    control = control_params)

Variables actually used in tree construction:
[1] BMI  FLCΣ LAB 

Root node error: 335/576 = 0.5816

n=576 (8 observations deleted due to missingness)

        CP nsplit rel error xerror     xstd
1 0.041791      0   1.00000 1.0000 0.035341
2 0.022388      1   0.95821 1.0478 0.034953
3 0.020896      3   0.91343 1.0179 0.035209
4 0.014925      5   0.87164 1.0090 0.035277
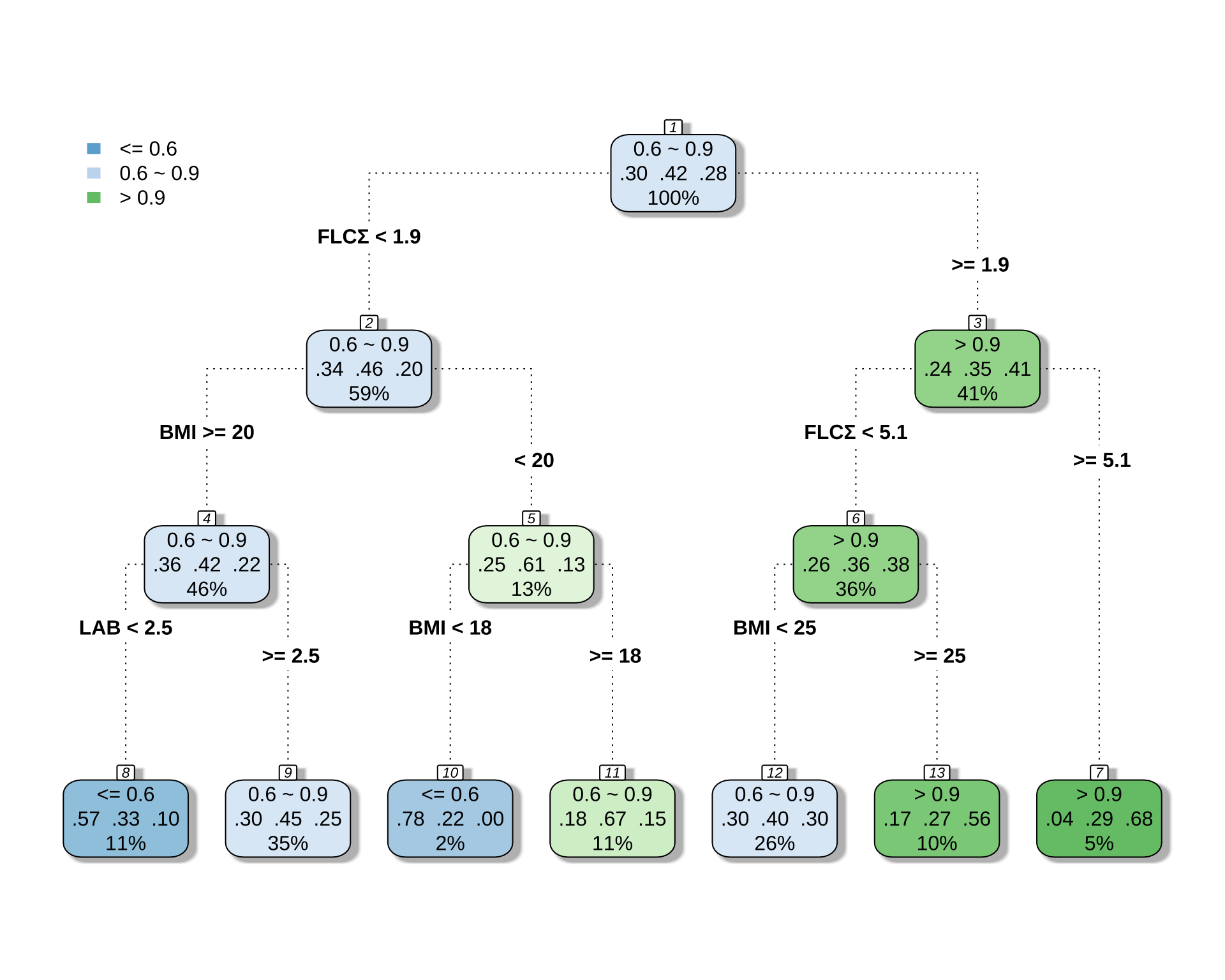
5 0.010000      6   0.85672 1.0119 0.035255

# 決定木を可視化
rpart.plot(
  cart_model,
  type = 4,           # ノードの表示スタイル
  extra = 104,        # 各ノードに所属するクラスの割合を表示 (例: L/M/H -> 239/12/0)
  box.palette = "BuGn", # カラーパレット
  branch.lty = 3,     # 枝の線の種類
  shadow.col = "gray", # 影の色
  nn = TRUE           # ノード番号を表示
)

# 予測値を取得
predictions <- predict(cart_model, newdata = df_filtered, type = "class")

# 混同行列を作成
confusion_matrix <- table(Actual = df_filtered$BP_level, Predicted = predictions)
print(confusion_matrix)

           Predicted
Actual      <= 0.6 0.6 ~ 0.9 > 0.9
  <= 0.6        42       118    11
  0.6 ~ 0.9     22       195    24
  > 0.9          6       106    52

# 正答率を計算
accuracy <- sum(predictions == df_filtered$BP_level, na.rm = TRUE) / sum(!is.na(df_filtered$BP_level))
cat("正答率:", round(accuracy * 100, 2), "%\n")

正答率: 50.17 %

2 BART による変数選択

2.1 モデル構築

df_filtered <- df %>%
  filter(is.na(BP備考)) %>%
  select(-c(BP備考, LOX_Index, 判別式, id, med_col, 年代, BP_level, BP_flag))

library(dbarts)

# 説明変数と被説明変数を準備
x_vars <- df_filtered[, !(names(df_filtered) %in% "BP")]
y_var <- df_filtered$BP

# 欠損値を含む行を削除
complete_cases <- complete.cases(x_vars, y_var)
x_vars_clean <- x_vars[complete_cases, ]
y_var_clean <- y_var[complete_cases]

# BARTモデルの実行
bart_model <- bart(
  x.train = x_vars_clean, 
  y.train = y_var_clean,
  # power = 5.0,
  # base = 0.7
)

summary(bart_model)

                Length Class  Mode   
call                 3 -none- call   
first.sigma        100 -none- numeric
sigma             1000 -none- numeric
sigest               1 -none- numeric
yhat.train      546000 -none- numeric
yhat.train.mean    546 -none- numeric
yhat.test            0 -none- NULL   
yhat.test.mean       0 -none- NULL   
varcount         21000 -none- numeric
y                  546 -none- numeric
n.chains             1 -none- numeric

2.2 変数選択

# 1. 変数ごと（列ごと）に使用回数を合計する
# colSums() を使って、1000回のMCMCステップでのカウントを各変数について合計します。
var_importance_scores <- colSums(bart_model$varcount)

# 2. 結果を重要度の降順でソートする
sorted_importance <- sort(var_importance_scores, decreasing = TRUE)

# ソートされた結果の確認
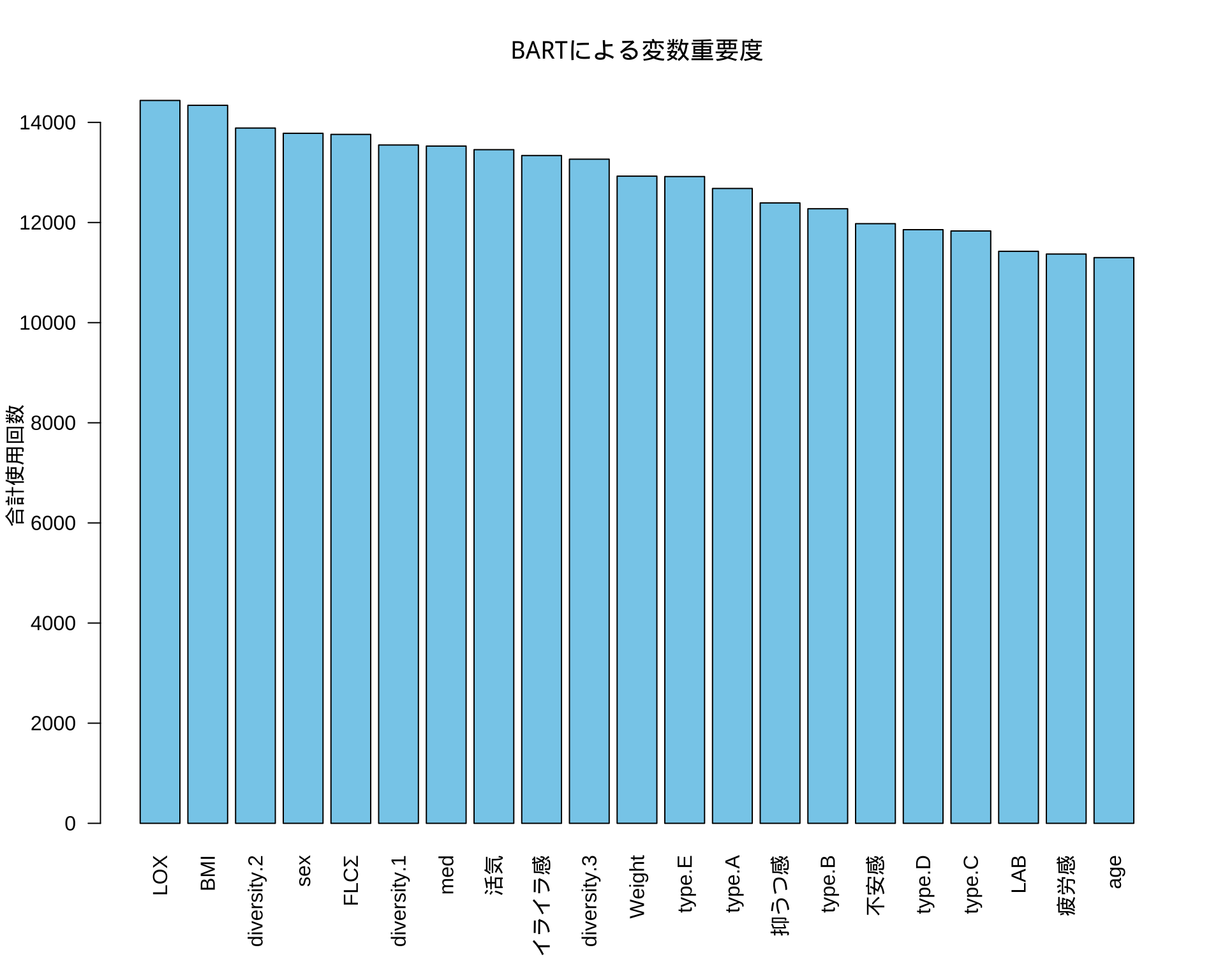
print(sorted_importance)

        LOX         BMI diversity.2         sex        FLCΣ diversity.1 
      14438       14341       13887       13782       13760       13548 
        med        活気  イライラ感 diversity.3      Weight      type.E 
      13527       13455       13338       13265       12926       12918 
     type.A    抑うつ感      type.B      不安感      type.D      type.C 
      12680       12391       12275       11977       11857       11831 
        LAB      疲労感         age 
      11425       11370       11299

# 3. barplot() を使ってプロットする (より見やすいプロット)
# barplot() の方がこの種のデータには適しています。
# las=2 は、変数名が重ならないように軸ラベルを垂直にします。
par(mar = c(6, 4, 4, 2) + 0.1) # 下側のマージンを広げてラベルを表示
barplot(sorted_importance, 
        las = 2, 
        main = "BARTによる変数重要度",
        ylab = "合計使用回数",
        xlab = "",
        col = "skyblue")