これからはじめるベイズ機械学習

所信表明を兼ねて

AI
著者

ぷに

日付

3/20/2024

現在，産業界における “AI” というと専ら，いくつかの限られた巨大 IT 企業が，巨大ニューラルネットワークを最尤推定で学習させ，これを基盤モデルとして公開し，我々一般庶民はそれを有効活用して下流タスクを安価に解くことだけ考えるという営みを指す．

その産業や生活への破壊的な影響を憂慮しながらも，雨乞いをする日々である．

図 1: 3月19日時点，GPT-5 にも Sora にもアクセス権を持たない我々 v.s. Lex Fridman Podcast に出演した Sam Altman

AI はそんなものではない．AI はこれにかぎるものではない．

AI が真に我々の友となり，我々の日常をほんとうに豊かにするは，AI の進歩だけが必要なのではなく，人間との協業が得意になる必要がある．

そのための第一歩はすでに明らかである．不確実性の定量化 である．

つまり，「その AI には何が出来て何が出来ないか」「AI の出力がいつ信頼にたるもので，いつ人間の介入が必要であるのか」がわかりやすい形で伝わるコミュニケーション様式をそなえている必要があるのである．1

筆者の知る限り，ここにある全てのナラティブは現時点では全く広く語られているものではなく，筆者も最初の１年の研究生活を通じて朧げながら見えて来たばかりのものである．

不確実性の定量化は，機械学習モデルを民主化し，我々の民芸に取り込むための重要な一歩である（のではないだろうか？）．

本稿はこの発見を共有するために書いた．筆者の反芻不足から，冗長な部分も多いだろうが，少しでも，琴線に触れるものがあれば幸いである．2

1 ベイズ機械学習のすすめ

我々が AI をより信頼するためには，何が必要だろうか？

筆者の考えでは，信頼への第一歩は 不確実性の定量化 が出来るようになることのはずである．

そしてそのためには ベイズ機械学習 (Bayesian Machine Learning) の発展による本質的解決が必要不可欠である．本稿はこの点を説明するために執筆されたものである．

筆者に言わせれば，ベイズ機械学習が，今後数年間で AI が経験すべき進展の方向である．この山を越えれば，今まででさえ思っても見なかった未来がひらけてくるだろう．

Although considerable challenges remain, the coming decade promises substantial advances in artificial intelligence and machine learning based on the probabilistic framework. (Ghahramani, 2015, p. 452)

1.1 ベイズとは何か？

機械学習において，確率論的なモデリングに基づいたアプローチを ベイズ機械学習 ともいう．典型的には，モデルの全変数上の結合分布をモデリングし，ベイズ規則によりパラメータのベイズ推定を行う，という手続きからなる．そのため，確率論的アプローチ や モデルベースアプローチ も同義語として用いられる．3

一方で，頻度論的 という言葉は，よく非ベイズ的アプローチを示す接頭辞として用いられる．典型的には，損失関数を設定し，これを最小化するパラメータを探索することによって実行される．

この２つのアプローチは互いに対照的であり，統計学の始まりから基本的な二項対立の図式をなしてきた．

Contrast of the two main approachs to Machine Learning
Bayesian Frequentist
Inference is4 Marginalization Approximation
Computational Idea5 Integration Optimization
Objective Uncertainty Quantification Recovery of True Value
Emphasis Modelling Inference

しかし，機械学習の時代においては，互いの弱みを補間し合う形で発展していくと筆者は考える．特に，現状の推論偏重でモデリング軽視の風潮が，重要な実世界応用の多くを阻んでしまっている．機械学習の世界樹は実は２本あるのである．

1.2 ベイズと頻度論との違い

ベイズと頻度論では，確率の解釈も異なるかも知れないが，数学的枠組みとしてはベイズの方が一般的な枠組みであり，また手続き上は，モデリングを重視するか，推論を重視するかの違いでしかない．

実際，殆どの場合，頻度論的手法はある特定の事前分布を持ったベイズ手法とみなせ，逆も然りである．

データから推論を行うには，何らかの仮定が必ず必要であり，それを明示的にモデルに組み込むのがベイズで，推論アルゴリズムにより自動化する精神を持つのが頻度論的手法である．

その結果，優秀な推論アルゴリズムが日夜驚異的なスピードで提案され，今や機械学習手法は教師あり学習・教師なし学習・強化学習の全てで目覚ましい発展を見た．

しかし，ベイズと頻度論の２つの柱のバランスを欠いた発展はここまでである．今や，頻度論的な手法を採用した際に，自分たちがどのような仮定を置いたのか全く明瞭な知識を欠いてしまっている．一方で，現実のビッグで複雑なデータを扱うためには，もはや確率的なモデリングを避けては通れない．6

極めて本質的で強大な敵に対面しつつあるのである．

だが，現状の病理は明らかであり，頻度論とベイズの手法の間に対応をつけ，足並みを揃えることで次の前進が約束されてる．この意味で，２つの世界樹が必要なのである．

さらに，ベイズ推論は帰納的推論の確率論的拡張と見れるため，エージェントの合理的な学習と意思決定の最良のモデル（の一つ）と信じられている．7

したがって，ベイズ流解釈により手法を理解し，最適化流解釈により手法を実装する．これがあるべき機械学習の未来であると筆者は考える．

1.3 ２つの世界樹

今こそ，この２つの手法は根底では繋がっていることをよく周知し，この２つの視座を往来しながら適材適所に使うことが大事だと筆者は考える．

しかしそのためには，ベイズ機械学習の発展が遅れている現状を鑑みて，ベイズの手法のより一層の発展と理解の深化が必要である．8

本章「ベイズ機械学習のすすめ」は，ベイズの手法の特に肝心と思われる３つの側面を指摘して終わる．以下３章を通じて，

  1. 第 2 節 ベイズは不確実性を定量化する

    Bayes の方が不確実性の定量化が得意であるため，そのような応用先では頻度論的な手法よりも，Bayes バージョンの手法を用いることが出来ると便利である．

  2. 第 3 節 ベイズは分布という共通言語を与える

    Bayes による統一的な扱いが理論的に有用である場面が増えている．その際に，Bayes による理論解析と最適化による実際の推論という適材適所の協業が未来の方向であるかも知れない．

  3. 第 4 節 ベイズは理解を促進する

    ベイズの手法が敬遠されていた理由も，換言すれば，「事前分布」という得体の知れないものを通じて，理論的深淵と直結するためである．ベイズ手法の研究が理論的な解明を要請する．だからこそ，数学者の魂を持った者がこの途を通ることは人類に大きく資すると筆者は考える．

2 ベイズは不確実性を定量化する

2.1 不確実性の定量化の必要性

機械学習と統計学が単なる道具ではなく，人間のより大きなシステムの一環を単独で担う場面が増えてきた．例えば，

  • 金融・経営・政策決定などの分野で，意思決定に繋げるデータ解析をするとき
  • 科学において，発見や仮説を検証するためのデータ解析をするとき
  • ロボットや自動車などの自動化をし，社会に実装するとき9
  • 医療診断や裁判などの場面で，専門家を補助するシステムを作るとき

これらのいずれの例でも，システムの一部を担うにあたって，不確実性を定量化しておくことが欠かせない．その出力を用いるのが人間である場合も勿論，別の機械学習モデルである場合は尚更である．

つまり，人間社会で優秀であるだけでなくホウレンソウと信頼獲得も重要であるように，機械学習モデルも性能の高さと正確さだけでなく，いつその結果を信頼して良いのかを「どの程度」という指標と共に知らせてくれることが信頼関係の基本となるだろう．

実際，殆どの場面で，データから高い確証度で言えることと，そうではないことでは全く違う意味を持つ．それぞれの場面での例には，次のようなものがあるだろう：

  • データから高い確証度で言えることと，意思決定者による采配が必要な部分を分離できない限り，意思決定プロセスの一部として組み込むことが難しく，結局機械学習手法が全く採用されないということもあり得る．
  • 結果の再現可能性が科学の基本的な要請である以上，その結果の不確実性を実験結果に付記することは基本的な科学的態度である．後述（第 2.3.1 節）するが，\(p\)-値や信頼区間などの統計量はこれに応えるものではない．
  • ロボットや自動車の自動化 AI システムは，いくつかのモデルを組み合わせて作ることになるだろう．個々が十分な性能を持っていても，小さな誤差が累積してシステムとしての性能を著しく低下させることがある．これを防ぐために，統一した方法での不確実性の取り扱いが必要である．
  • 個々人の権利と法益が衝突する場面にも AI が利用されより良い生活が実現されるには，法的な解釈可能性が担保される必要があることが，実は大きな難関として我々を待っている．その第一歩は，不確実性の可視化になるだろう．10

以上の内容は，結果の 解釈可能性 でも全く同じことが言えるだろう．

2.2 信頼のおける AI システム

上述の点をまとめると，機械学習手法と人間社会がよりよく共生していくには AI の 信頼性 (trustworthyness) が必要とされているのである．不確実性の定量化と解釈可能性は，AI が人間社会で信頼を獲得するにあたって根本的な要素になるだろう．

現状の手法の延長でこの信頼性の問題は扱えず，新たな手法が必要とされている．Bayesian approach や probabilistic approach と呼ばれている試みは，まさにこれに応えるものであり，近年急速に発展している．

2.3 不確実性を扱うには Bayes が必要である

実装は頻度論的な手法の方が簡単で高速であることが多いが，不確実性の定量化には向かない．

このような場面では，頻度論的手法を頻度論的に改善する，という方向は筋が悪いと思われる．このようなときこそ，もう一つの世界樹であるベイズの方法を用いるべきである．

これを，科学における再現性の危機を例にとって確認したい．11

2.3.1 再現性の危機

多くの実験科学では不確実性の定量化が必要不可欠である (Krzywinski and Altman, 2013)．

It is necessary and true that all of the things we say in science, all of the conclusions, are uncertain … (Feynman, 1998)

再現性の危機 (replication crisis) とは，多くの実験において報告されている統計的有意性が，再現実験において得られないことが多いという問題を指し，2010年代の初めから多くの科学分野において問題として取り上げられてきた．12

その理由は明白である．信頼区間は集合値の推定量であるため，「分散」が十分大きいならば，データセットを変えて何回も計算することでいずれは非自明なものを得ることが出来るのである．そのため，信頼区間や \(P\)-値を報告するだけでは，結果の信頼性については何も保証されないのである．

その結果多くの科学分野では Bayes 統計学による不確実性の定量化に移行しつつある (Herzog and Ostwald, 2013), (Trafimow and Marks, 2015), (Nuzzo, 2014)．

信頼区間と信用区間の違いに注目して，その違いを解説する．

2.3.2 信頼区間と信用区間

「95 % の信頼区間」と言ったとき，「95 % の確率で真の値がその範囲に含まれるような区間」だと思いがちであるが，これはどちらかというと信用区間の説明であり，信頼区間は計算するごとに値が変わってしまう確率変数である ことを見落としがちである．13

つまり，信頼区間は頻度論的な概念であり，「真の値」がまず存在し，区間自体が変動し，95 % の確率で被覆するというのである．今回見ている信頼区間が，別のデータセットで計算した場合にどう変わるかについては全く未知である．

このことは，信頼区間は「真のパラメータの値」で条件づけて得るものであるが，信用区間はデータによって条件づけて得るものであるという点で違う，とまとめられる．この２つの混同は「何で条件づけているか？」を意識することで回避することができる．14

誤解を恐れず言うならば，再現性の危機とは，信頼区間というサイコロの出目によって科学が踊らされていたということに他ならない (Nuzzo, 2014)．15

2.3.3 なぜベイズを用いれば良いのか？

これは，信頼区間や \(P\)-値などの頻度論的な手法は，しばしば尤度原理に違反するためである．16

換言すれば，何らかのモデルと事前分布に関するベイズ手法と等価である，すなわち，Bayesianly justifiable (Rubin, 1984) とみなせない手法は，何らかの意味でデータを十分に反映できていない可能性が高くなる．

従って，ベイズの手法が原理的に最も適切である場面が多い．一方でその計算の困難さや，全てのステップをモデリング段階に組み込む点を回避するために，種々の頻度論的な実装は考え得て，頻度論的な手法はそのような運用においては健全であるとの指標にもなる．17

Bayes により手法を理解し，頻度論的に手法を実装することが，あるべき姿勢であると思われる．

The applied statistician should be Bayesian in principle and calibrated to the real world in practice. (Rubin, 1984)

2.4 ベイズ深層学習という夢

深層モデルはその性能の高さから，最も実世界応用が期待されるモデルであるが，パラメータが極めて多いため，特にベイズ化することが難しいと言われている．

例えば，ハルシネーション (hallucination) として，LLM が「事実に基づかない」情報を生成してしまうことが問題とされているが，これも不確実性の定量化の問題に他ならない．18

その他の場面でも，不確実性の定量化には conformal prediction などの事後的な手法が試みられている．19 これらはどのようなブラックボックスに対しても適用可能である一方で，対症療法というべきものであり，ベイズ流の解釈をすることで直接的に事後分布を求めるという根本的な解決にも，もっと注力されるべきである．

ベイズによる不確実性の定量化は，自然であるだけでなく，より有用な不確実性の定量化を与えるものだと予想している．20

加えて，事前分布を変えることで，種々の帰納バイアスを加えるという「プロンプトエンジニアリング」ならぬ「プライヤーエンジニアリング」の理論が樹立できるかもしれない．すでに，公平性，同変性，スパース性，共変量シフトへの頑健性などを達成するための事前分布が考えられている．21

2.5 分野全体の動向

現状の機械学習モデルと実応用との乖離は，他の側面でも生じている．

まず，訓練データが実際の運用環境を十分に反映できていないということは極めて頻繁に起こるだろう．この現象を 分布シフト といい，機械学種モデルの予測性能だけで無く，分布外汎化 (out-of-distribution generalization) 能力も重視するという潮流が生じている．

さらに，一度訓練したモデルを，分布シフト自体が移り変わっていく環境で，微調整のみによって繰り返し使い続けるという使用を想定した 継続学習 (continual learning) という考え方もある．22

章を変えて別の角度から議論を続けよう．

3 ベイズは分布という共通言語を与える

3.1 継続学習という発想

継続学習は，機械学習モデルをより動的で実際的な環境でも使えるようにするための新たな枠組みである．そこまで，教師あり学習モデルがすでに実用的な性能を獲得したということでもある．

つまり，単に「教師あり」「教師なし」の１タスクを解く営みは爛熟しつつあり，機械学習の理論と応用の最先端は，より深い森に分け入りつつあるのである．

ここにおいて，ベイズ流の接近が統一的な取り扱いを与えるという美点が，さらに重要でもはや必要不可欠な役割を果たすものと思われる．

3.1.1 ベイズ推論が与える統一的枠組み

ベイズ推論とは，事前分布 というものを設定して，これをデータによって更新するという営みである（その更新規則は Bayes の公式が与える）．

事前分布をどう設定すれば良いか？の問題は，ベイズ推論の初期からの問題であった．極めて自由度が高いことが，逆にベイズ推論が実際のデータ解析の場面において敬遠される一因ともなっていた．

3.1.2 ベイズと最適化との協業

しかし，継続学習が当たり前になった社会において，全てのパラメータ値を事前分布と事後分布とみなし，全ての学習過程をベイズの公式という統一的な方法で更新すると捉えられることは，極めて大きな利点になり得る．

というのも，継続学習においては，学習を繰り返すうちに過去に学んだ内容を忘れ去ってしまうという 壊滅的忘却 (catastrophically forgetting) が最大の困難である．

理論的には，分布のベイズ更新の繰り返しとして見る方が極めて見通しが良い．一方で，事後分布の近似が十分でない場合，実際にベイズ更新を行うことは性能に悪影響を与える．

そこで，理論解析や設計をベイズの観点から行い，実際の推論は最適化ベースで行うという適材適所により，壊滅的忘却を緩和できる可能性がある (Farquhar and Gal, 2019)．

3.2 例：強化学習への分布によるアプローチ

we believe the value distribution has a central role to play in reinforcement learning. (Bellemare et al., 2017)

4 ベイズは理解を促進する

我々はもはや機械学習を通じて，自分たちが何をやっているのかわかっていない．この愚かさを AI に継がせてはならない．

4.1 なぜベイズ法の発展が遅れたか？

ベイズ法の採用は，自分たちが何をやっているかへの理解と解釈可能性を刺激するという側面がある．

その理由は簡単である．ベイズ推論は，モデルとその上の事前分布を定めれば，あとはベイズ更新規則をどう計算するかの問題となり，近似手法は様々あれど，もはや推論手法に選択の余地はない．

換言すれば，その分解析者がモデルと事前分布の特定を全てこなす必要があるのであり，解析者に確率モデリングへの理解を強要するところがある．

しかしこれは「面倒なことは全てアルゴリズムにやってほしい」という精神とは対立するため，ベイズの美点であると同時に，ベイズの発展を阻害してきた遠因の一つでもあった．

これを指して「事前分布の選択に恣意性が入る」という通り文句がよく使われるが，実際は，頻度論的手法における「どのような目的関数をどのように最適化すれば良いか？」という恣意性に変換されているのみであり，問題を先送りにして，「ベイズ法 対 頻度論的手法」という虚構の対立を作り上げているのみである．

機械学習のポテンシャルが具現化したいまこそ，この困難に立ち向かう必要があるが，この問題は最適化や頻度論的な立場から見るより，ベイズの立場から見た方が，理論的な見通しが良いようである（第 4.4 節）．

4.2 帰納バイアスの明確化の必要性

機械学習の真の理解のためには，各モデルの帰納バイアスを明確化する必要がある．

4.2.1 帰納バイアスとは何か？

現状の AI システムは大量のラベル付きデータが必要であり，多くの現実的に有用なタスクでこのような教師データが用意できるわけではない．

一方で，人間は遥かに少ないデータから効率的に学習することができる．

Number of Training Tokens BabyLM Challenge

その違いは，進化が我々生物に授けた 帰納バイアス にあると考えられている．

我々には遺伝的に継がれている生まれ持った学習特性があり，より効率的に学習出来るのかも知れない．

事実，一度事前学習をした LLM は，極めて少ないデータにより新しいタスクを学習することができるがわかりつつある (Zhou et al., 2023)．LLM の事後調整に関する稿 も参照．

4.2.2 事前分布に向き合わずにやり過ごしてきた

現状，多くの機械学習手法は確率的な方法を取っていない．これは事前分布を明示せずに（ひょっとしたら明後日の方向に向かって）行われる Bayes 学習手法であるとみなせる．

現状の機械学習の成功は，事前分布に関する知識なしに到達されたものであり，それ故の限界がある．例えば，現状のままではモデルにどのような帰納バイアスが組み込まれているか不明瞭である．23

4.2.3 帰納バイアスに対するベイズ的視点

データの空間 \(\mathcal{X}\) 上の任意のモデル \(\mathcal{M}\) の周辺尤度 \(p(x|\mathcal{M})\) は，24 ベイズ流には事後確率として捉えられ，全てのデータ \(x\in\mathcal{X}\) 上に有限な測度を定める．25

よって，全てのモデルは，あるデータを得意とするならば他のデータについては不得意であることを免れない．これは no free lunch 定理と呼ばれる定理の一群により推測されており，分類問題などの簡単なタスクを除いて完全な形式的表現はまだ持たない作業仮設である．

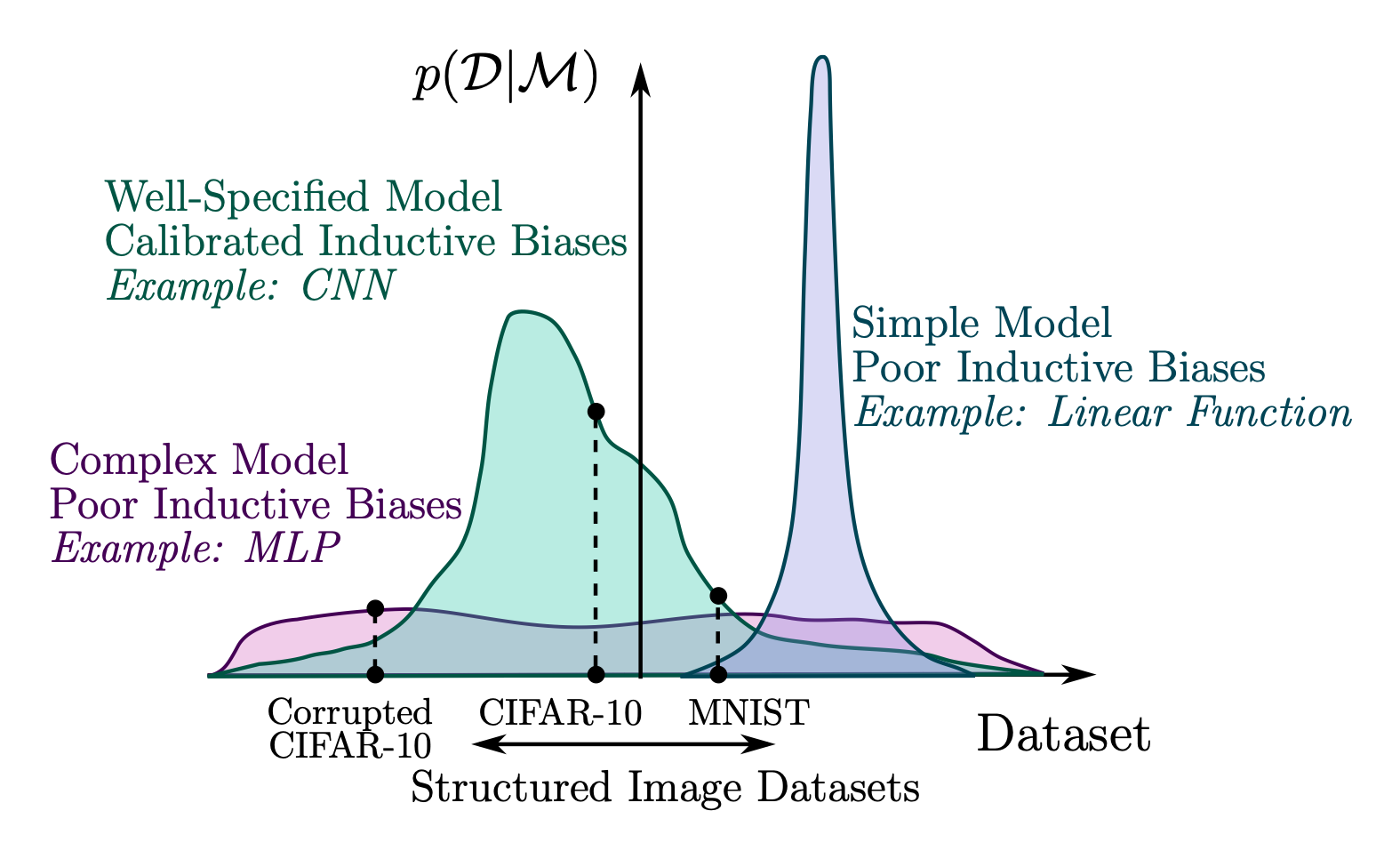
A Probabilistic Perspective of Genelization (Wilson and Izmailov, 2020)

例えば，基盤モデル とは，インターネット上のデータから最大限人間の言語というものに関する帰納バイアスを取り込んだ，パラメータ上の初期設定であると見れる．

これは，あるパラメータ空間上の理想的な事前分布からのサンプリングであるかも知れない．それ故，種々の下流タスクに対して，小さなモデル変更のみにより適応することが出来る．

大規模言語モデルの能力創発現象は，帰納バイアスを十分取り込むことにより自然に解かれるタスクであったのかもしれない．

4.2.4 worst-case analysis からの脱皮

帰納バイアスを明確にせず，やり過ごしてきたつけが，特に学習理論においても現れている．

現状の統計的学習理論は全て，worst-case analysis であるが，実用上は全くそうではない．「動くモデル」には暗黙の帰納バイアスが入っており，これに明るくなる必要があるのである．

2024 年に生きる我々は，worst-case analysis からの脱皮を迫られている．

4.3 数学者の哲学

Bayes の見方は，機械学習モデルを底流する数理的枠組みになっている．仮に次の Mac Lane の言葉が数学者のあるべき態度の１つであるとするならば，この意味での数学者には Bayes の立場から機械学習を研究することを特におすすめする．

However, I persisted in the position that as mathematicians we must know whereof we speak, be it a homotopy group or an adjoint functor. (Mac Lane, 1983, p. 55)

数理統計学に始まり，数学者の統計や機械学習分野への参入は，推論手法の解析が想像されるかも知れない．

しかし，真の数学的理解は，手法の数学的な機械仕掛けを紐解くだけでなく，それぞれの手法がモデルとしてどのような仮定の下で成り立っているかを，モデリングの観点から理解することにもあると筆者には思われる．

現状，後者の視点が大変に不足しており，数理的な知識に支えられた大局観というものがない．個々の数学的な道具に捉われず，大局的な構造を捉える数理的枠組みが必要である．

これに応えるのがベイズの枠組みであると筆者は信じる．

推論とモデリングという双対的な営みは深い数理的な構造を持っていることが明らかになりつつある．この大局的構造の解明と理論構築には，ベイズの観点から光を照らしてくれるような，Mac Lane の意味での数学者的な魂が必要とされているのである．

4.3.1 Bayes の数学

Bayes 流の解釈では，どんなにモデルが複雑で巨大になろうとも，推論とは積分に他ならない．

Bayes’ Theorem (density form)

全ての（尤度原理に則った）推論は，事後分布の関数としてなされる（べきである）．

実際の実装は，その近似として実行される（べきである）．

よって，実装とモデリングの段階を明確に分離する枠組みを提供している上に，極めて普遍的な枠組みである．

というのも，Bayes 流のモデリングは，Markov 圏 上の図式と見ることができ（第 5.2 節），普遍的である上に，数学的にも最も直接的で直感的な表現であると思われる．

圏として持つ代数的性質は，モデルの結合・分解が自由に出来るということに繋がり，モジュール性 が高いということになる．

I basically know of two principles for treating complicated systems in simple ways: the first is the principle of modularity and the second is the principle of abstraction. I am an apologist for computational probability in machine learning because I believe that probability theory implements these two principles in deep and intriguing ways — namely through factorization and through averaging. Exploiting these two mechanisms as fully as possible seems to me to be the way forward in machine learning. Michael I. Jordan excerpted from (Frey, 1998)

分布を明示的に用いた 確率核 を通じてのモデリングは，なぜだか数学的に極めて自然なアプローチを提供してくれるようである．

4.3.2 ベイズの代数・幾何・解析

上述したように，ベイズのモデリング法と学習規則は本質的に代数的なところがある．

加えて，分布を基本言語とするために，ベイズ推論においては空間 \(\mathcal{P}(\mathcal{X})\subset\mathcal{M}^1(\mathcal{X})\) が極めて基本的な役割を果たす．

サンプリングは \(\mathcal{P}(\mathcal{X})\) 上の幾何学に関係が深く，情報幾何学や最適輸送などの発展が見られている．

一方で最適化は \(\mathcal{P}(\mathcal{X})\) 上の解析学に関係が深く，古くから機械学習分野では \(\mathcal{P}(\mathcal{X})\) 上の様々な汎函数が ダイバージェンス の名前で考察されており，その勾配流として種々の最適化手法が理解できる．

4.3.3 Bayes に繋げる数学

通常の頻度論的手法は，うまくいくことが先であり，理論が後付けされる．そしてその理論もどこか ad-hoc というべきであり，worst-case で漸近論的である．

これらに Bayes 的な解釈を与えることで，暗黙のうちにどのような仮定を課しているモデリング手法に相等するのか明確にされる．特に，非漸近論的な知見を与えてくれる数少ないの道の一つである．

4.4 ベイズ推論とみる美点

ベイズ推論自体への理解だけでなく，種々の頻度論的手法を（特定の環境下での）ベイズ推論の近似として理解することは，新たなアルゴリズムの開発に有用であるという合意が形成されつつあるようである．26

最適化に基づく手法の計算効率性は，正確なベイズ推論に勝る場面も多い．ここで注意すべきは，ベイズ推論の実行が肝要であり，その実装は最適化に依ろうと，積分近似に依ろうと大した違いではないのである．

「ベイズ推論は多くの最尤法に基づく手法よりも，自然な正則化がなされるために過学習の問題がない．」と説明されるが本来は逆である．多くの最適化に基づく手法は，目的関数の選択に恣意性があり，その選択を誤り続けているために過学習という問題が生じている，という方が，後世の教科書に載る表現なのではないかと筆者は考えている．

そこで，種々の既存手法のベイズ流の解釈を探究することは，より良い推論アルゴリズムの開発に資すると考えられている．

この方向の近年の発展をいくつか紹介したい．

4.4.1 ベイズ学習規則

現状の機械学習は，統計学，連続最適化，計算機科学の知識を総動員して開発された種々の推論手法によって支えられている．

その性能は驚異的なスピードで向上しているが，それぞれの手法がどのような仮定をモデリングの段階で課しているかが不明瞭であり，どの手法を使うべきかの統一的な枠組みは得られていない．

この現状の抜本的な改善が，それぞれの手法のベイズ流の解釈を探究することで得られると考えられる．

その枠組みの一つが ベイズ学習規則 (Khan and Rue, 2023) である．

(Khan and Rue, 2023, p. 4) では，ベイズ流の解釈を持つ種々の手法が他より優れている理由として，目的関数に現れるエントロピー項が 自然勾配 の概念を通じて自然な正則化を与えることが，ベイズ学習規則という新たな理論的枠組みの中で示されている．

4.4.2 例：強化学習

強化学習でも，モデルベースのアプローチが取り入れられつつあり (Deisenroth and Rasmussen, 2011)，さらに学習と制御をベイズ推論と見ることが，アルゴリズムの設計において有用であることが提唱されつつある：

Crucially, in the framework of PGMs, it is sufficient to write down the model and pose the question, and the objectives for learning and inference emerge automatically. (Levine, 2018)

5 Bayes 機械学習の例

要約

深層学習モデルにより教師あり学習は十分に発展し，多くの訓練データが得られる場面では驚異的な性能を発揮するようになった．

この発展は，モデリングの仮定に捉われずに純粋にアルゴリズムの開発に集中することが出来るという頻度論的な枠組みの利点を有効活用する形で達成された．

しかし，殆どの実世界応用では，不確実性のモデリングが必要不可欠である．この点を後回しにして性能を追求することで得た栄華である．だからこそ，極めて高い性能を誇るモデルを，実世界応用の場面で有効活用する手段を我々はまだ知らないのである．

その鍵はベイズにある．安全性，信頼性，柔軟性……．これらの21世紀の社会の要請に応えるためには，ベイズ機械学習手法の発展と，既存の手法のベイズ流の理解とが追いつくことが，第一歩である．

既存の深層学習モデルは，「教師あり学習」という枠組みや，画像の分類タスクや自然言語処理のタスクなど，広く周知された問題設定とデータセットが存在する．

一方で，ベイズ機械学習における対応物はまだ十分に周知されていないようである．

ベイズ機械学習では「損失を最小化する」という枠組みの中でなるべく性能の良い推論手法を探す，というわかりやすい枠組みがある訳ではないようである．

そこで，本章ではベイズ機械学習の近年の発展を概観することを試みる．

5.1 Bayes 深層学習

ニューラルネットワークモデルは，隠れ素子数が無限大になる極限において，Gauss 過程モデルに漸近することが知られている (Neal, 1996)．Gauss 過程とはノンパラメトリックなベイズ機械学習手法の代表である．この対応を通じて，深層学習のベイズ流の解釈が進められている．

この稿の執筆後，本稿をまとめるかのようなアブストラクトを持ったポジションペーパー (Papamarkou et al., 2024) が公開された

In the current landscape of deep learning research, there is a predominant emphasis on achieving high predictive accuracy in supervised tasks involving large image and language datasets. However, a broader perspective reveals a multitude of overlooked metrics, tasks, and data types, such as uncertainty, active and continual learning, and scientific data, that demand attention. Bayesian deep learning (BDL) constitutes a promising avenue, offering advantages across these diverse settings. (Papamarkou et al., 2024)

深層学習をベイズ化することで，上にあげた

  • 不確実性の自然な定量化
  • 継続学習への柔軟な接続
  • 科学的営みの促進

などが目指せる．特に，現状の大規模な基盤モデルをベイズ化する悲願を真っ向から論じている．

5.2 確率的グラフィカルモデル

歴史的に，（確率的）モデリングは，主に（確率的）グラフィカルモデルを通じて機械学習の分野に導入された．

そのため，20世紀に入ったばかりの頃は，Bayes 機械学習の唯一の例は確率的グラフィカルモデルなのであった．27

だが，確率的グラフィカルモデルは，極めて普遍的で，従来の因果推論・階層モデル・欠測モデル・潜在変数モデル・構造方程式モデルなどの発展を包含する統一的な枠組みであることをより広く認識すべきである．

5.2.1 ベイジアンネットワーク

Bayesian Network は Markov 圏上の図式であり，方向関係のある変数間の関係をモデリングする最も直接的な方法である．

5.2.2 構造的因果モデル

5.2.3 階層モデル

階層モデルとは，ベイズの枠組みでは，観測変数・潜在変数の区別なく，モデルを自由に結合出来る点を利用したモデリング手法である．

5.2.4 モデルの属人化

大きなデータも，属人化医療や推薦システムなど多くの文脈では小さなデータの寄せ集めであり，そうでなくともその構造を正しく捉え，全ての不確実性を取り入れた柔軟なモデリングをすることで，さらに密接な形で社会に取り入れることができる．28

5.3 確率的プログラミング

5.3.1 アルゴリズムのプログラミングから，モデルのプログラミングへ

ベイズ流の解釈では，解析者の恣意的な選択はモデリングの段階に集中しており，モデルが決定すれば推論手法は自動的に従う．

このパラダイムでは，推論手法は背後に隠し，解析者はモデリングに集中するための新たなプログラミング言語があっても良いはずである．

このような言語を 確率的プログラミング (Probabilistic Programming) 言語と呼ぶ．

5.3.2 確率的プログラミングはグラフィカルモデルの拡張である

確率的グラフィカルモデルをどのようにプログラムに落とし込むかというと，確率核をシミュレーターとして実装するのである．

逆に，シミュレーションが可能な限りどのようなモデルも実装できるので，確率的グラフィカルモデルの真の拡張であると言える．29

5.3.3 Simulation-based Inference

上述の通り，シミュレーターがあればモデルが定義でき，モデルがあれば推論ができる．さらに，棄却法，重点サンプリング法，MCMC，SMC などの Monte Carlo 法のレパートリーにより，殆どあらゆるシミュレーションと推論が統一的に実行できる．これが Bayes 推論の強みである．

5.4 Bayes 最適化

ベイズはシステムの一部として自然に組み込まれると論じたが（第 2.1 節），現状その最先端をいくのがベイズ最適化の分野である．

ベイズ最適化は最も簡単な形では，未知の関数 \(f:X\to\mathbb{R}\) の最大値点を求める問題を，逐次意思決定問題 として解く手法である．

ベイズ数値計算 (O’Hagan, 1991) の現代的な再解釈とも捉えられる．30

この際，未知の関数 \(f\) を Gauss 過程などでモデリングし，不確実性の高い点からサンプル \(f(x_1),f(x_2),\cdots\) を取って最も効率の良い方法で最大化していくことを目指す．

ベイズ最適化は多腕バンディット問題と関係が深く，２つの問題は共に一方向のエージェント・環境相互作用しか仮定していないという形での強化学習への入り口である．

5.5 確率的データ圧縮

殆どの（可逆）データ圧縮アルゴリズムは，シンボルの列に対する確率的モデリングと等価である．31 そしてモデルの予測精度が良いほど，データの圧縮率は高い．

したがって，より良いベイズ（ノンパラメトリック）モデルの開発と，より幅広いデータに対するデータ圧縮技術の発展とは両輪である．32

5.6 モデルの自動発見

機械学習の精神の一つに，データからの知識獲得をなるべく自動化したいというものがある．

ベイズの方から，統計解析自体を自動化する Automatic Statistician (Lloyd et al., 2014) という試みがある．これはデータを説明するモデルを自動発見し，結果を自然言語でまとめてくれる上に，モデルに含まれる不確実性に関しても報告してくれる．

References

Amershi, S., Weld, D., Vorvoreanu, M., Fourney, A., Nushi, B., Collisson, P., … Horvitz, E. (2019). Guidelines for human-AI interaction. In Proceedings of the 2019 CHI conference on human factors in computing systems, pages 1–13. New York, NY, USA: Association for Computing Machinery.
Angrist, J. D., and Pischke, J.-S. (2010). The credibility revolution in empirical economics: How better research design is taking the con out of econometrics. The Journal of Economic Perspectives, 24(2), 3–30.
Bansal, G., Nushi, B., Kamar, E., Weld, D. S., Lasecki, W. S., and Horvitz, E. (2019). Updates in human-AI teams: Understanding and addressing the performance/compatibility tradeoff. Proceedings of the AAAI Conference on Artificial Intelligence, 33(01), 2429–2437.
Bellemare, M. G., Dabney, W., and Munos, R. (2017). A distributional perspective on reinforcement learning. In D. Precup and Y. W. Teh, editors, Proceedings of the 34th international conference on machine learning,Vol. 70, pages 449–458. PMLR.
Broderick, T., Gelman, A., Meager, R., Smith, A. L., and Zheng, T. (2023). Toward a taxonomy of trust for probabilistic machine learning. Science Advances, 9(7), eabn3999.
Chen, J., Monica, J., Chao, W.-L., and Campbell, M. (2023). Probabilistic uncertainty quantification of prediction models with application to visual localization.
Deisenroth, M. P., and Rasmussen, C. E. (2011). PILCO: A model-based and data-efficient approach to policy search. In Proceedings of the 28th international conference on international conference on machine learning, pages 465–472. Madison, WI, USA: Omnipress.
Efron, B. (1986). Why isn’t everyone a bayesian? The American Statistician, 40(1), 1–5.
Farquhar, S., and Gal, Y. (2019). A unifying bayesian view of continual learning.
Feynman, R. P. (1998). The meaning of it all: Thoughts of a citizen scientist. Addison-Wesley.
Frey, B. J. (1998). Graphical models for machine learning and digital communication. The MIT Press.
Gal, Y., and Ghahramani, Z. (2016). Bayesian convolutional neural networks with bernoulli approximate variational inference. In International conference on learning representations.
Ghahramani, Z. (2015). Probabilistic machine learning and artificial intelligence. Nature, 521, 452–459.
Herzog, S., and Ostwald, D. (2013). Sometimes bayesian statistics are better. Nature, 494(7435), 35–35.
Khan, M. E., and Rue, H. (2023). The bayesian learning rule. Journal of Machine Learning Research, 24(281), 1–46.
Krzywinski, M., and Altman, N. (2013). Importance of being uncertain. Nature Methods, 10(9), 809–810.
Levine, S. (2018). Reinforcement learning and control as probabilistic inference: Tutorial and review.
Lloyd, J. R., Duvenaud, D., Grosse, R., Tenenbaum, J. B., and Ghahramani, Z. (2014). Automatic construction and natural-language description of nonparametric regression models. In Proceedings of the twenty-eighth AAAI conference on artificial intelligence, pages 1242–1250. Québec City, Québec, Canada: AAAI Press.
Mac Lane, S. (1983). The health of mathematics. The Mathematical Intelligencer, 5(4), 53–56.
Mohri, C., and Hashimoto, T. (2024). Language models with conformal factuality guarantees.
Murphy, K. P. (2022). Probabilistic machine learning: An introduction. MIT Press.
Neal, R. M. (1996). Bayesian learning for neural networks,Vol. 118. Springer New York.
Neal, R. M., and Hinton, G. E. (1998). Learning in graphical models. In M. I. Jordan, editor, pages 355–368. Springer Dordrecht.
Novello, P., Dalmau, J., and Andeol, L. (2024). Out-of-distribution detection should use conformal prediction (and vice-versa?).
Nuzzo, R. (2014). Scientific method: Statistical errors. Nature, 506(7487), 150–152.
O’Hagan, A. (1991). Bayes–hermite quadrature. Journal of Statistical Planning and Inference, 29(3), 245–260.
Papamarkou, T., Skoularidou, M., Palla, K., Aitchison, L., Arbel, J., Dunson, D., … Zhang, R. (2024). Position paper: Bayesian deep learning in the age of large-scale AI.
Rubin, D. B. (1984). Bayesianly Justifiable and Relevant Frequency Calculations for the Applied Statistician. The Annals of Statistics, 12(4), 1151–1172.
Steinruecken, C., Ghahramani, Z., and MacKay, D. (2015). Improving PPM with dynamic parameter updates. In 2015 data compression conference, pages 193–202.
Trafimow, D., and Marks, M. (2015). Editorial. Basic and Applied Social Psychology, 37(1), 1–2.
Wang, L., Zhang, X., Su, H., and Zhu, J. (2024). A comprehensive survey of continual learning: Theory, method and application. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1–20.
Wilson, A. G., and Izmailov, P. (2020). Bayesian deep learning and a probabilistic perspective of generalization. In Proceedings of the 34th international conference on neural information processing systems. Red Hook, NY, USA: Curran Associates Inc.
Zhou, C., Liu, P., Xu, P., Iyer, S., Sun, J., Mao, Y., … Levy, O. (2023). LIMA: Less is more for alignment. In Thirty-seventh conference on neural information processing systems.
平石界, and 中村大輝. (2022). 心理学における再現性危機の10年―危機は克服されたのか，克服され得るのか―. 科学哲学, 54(2), 27–50.

Footnotes

  1. これは Human-AI interaction におけるガイドライン (Amershi et al., 2019), (Bansal et al., 2019) でも明確にされている点である．この方向への試みの代表がベイズ機械学習，というわけではないが，筆者はベイズ機械学習の興隆は信頼のおける AI システムの構築にための極めて盤石な土台になるだろうと論じる．↩︎

  2. 本稿執筆後に，ほとんど同じ論調を，深層学習や基盤モデルを中心に，遥かに明瞭に述べた論文 (Papamarkou et al., 2024) を見つけたので，賢明な読者はぜひこちらを参考にしていただきたい．↩︎

  3. (Broderick et al., 2023, p. 2) など．↩︎

  4. この違いが「過学習」という現象に見舞われるかの違いでもある．“Fortunately, Bayesian approaches are not prone to this kind of overfitting since they average over, rather than fit, the parameters” (Ghahramani, 2015, p. 454)．↩︎

  5. “for Bayesian researchers the main computational problem is integration, whereas for much of the rest of the community the focus is on optimization of model parameters.” (Ghahramani, 2015, p. 454)．このように，その用いる手法も鮮やかに対照的に見えるが，積分は変分近似を通じて最適化問題としても解けるし，Lengevin 法や HMC などの最適化手法は積分問題を解ける．↩︎

  6. (Broderick et al., 2023) が極めて説得的にこの点を指摘している．↩︎

  7. 合理的な信念の度合い (degree of belief) は確率の公理を満たす必要がある，という主張は Cox の名前でも呼ばれる．この点から，Bayes の定理は，帰納的推論の確率論的な拡張だとも捉えられる．“This justifies the use of subjective Bayesian probabilistic representations in artificial intelligence.” “Probabilistic modelling also has some conceptual advantages over alternatives because it is a normative theory for learning in artificially intelligent systems.” (Ghahramani, 2015, p. 453)．↩︎

  8. 現状，日本にてベイズ機械学習を専業として研究を進めている人は Emtiyaz Khan に限ると思われる．(Ghahramani, 2015, p. 452) でも “Probabilistic approaches have only recently become a mainstream approach to artificial intellifence, robotics, and machine learning.” と述べられている．↩︎

  9. “The uncertainty quantification of prediction models (e.g., neural networks) is crucial for their adoption in many robotics applications. This is arguably as important as making accurate predictions, especially for safety-critical applications such as self-driving cars.” (Chen et al., 2023)．↩︎

  10. モデルの予測結果に不確実性の定量化が伴われていたならば，モデルを信用出来ない場面で意思決定者がこれを信用したため責任があるのか，使用者には非難可能性がないのか，モデル設計者に過失があったと言えるのかの議論に，足場を与えることが出来るだろう．↩︎

  11. (Gal and Ghahramani, 2016) も参照．↩︎

  12. 心理学においては「再現性問題が大きく注目される大きな契機となった「超能力論文」が出版されたのが 2011 年である」 (平石界 and 中村大輝, 2022) ようである．計量経済学における 信頼性革命 (Angrist and Pischke, 2010) は，再現性の危機の，もう一つの革新的な解決法である．↩︎

  13. 「それでは，信頼区間は不確実性の正しい定量化を与えないではないか！」ということになるが，その通りなのである．\(P\)-値を計算する過程とは，帰無仮説で条件付けているだけであり，データの関数でもある．\(P\)-値の確率変数としての分散が大きいほど，何回か同じ実験を繰り返せばすぐに小さな \(P\)-値が得られることになる．これは 基準確率の誤謬 と似ている．↩︎

  14. “Confidence intervals suffer from an inverse inference problem that is not very different from that suffered by the NHSTP. In the NHSTP, the problem is in traversing the distance from the probability of the finding, given the null hypothesis, to the probability of the null hypothesis, given the finding.” (Trafimow and Marks, 2015)↩︎

  15. (Nuzzo, 2014) には，Fisher が最初に用いてから，Neyman-Pearson 理論がこれを排除したものの，コミュニティが \(P\)-値を誤解して都合の良いように利用するようになるまでに至った歴史が説明されている．↩︎

  16. (Murphy, 2022, p. 201) の議論も参照．↩︎

  17. (Efron, 1986) も示唆深い．↩︎

  18. (Mohri and Hashimoto, 2024), (Papamarkou et al., 2024, p. 3) 2.1節 なども指摘している．↩︎

  19. (Novello et al., 2024) では out-of-distribution detection, (Mohri and Hashimoto, 2024) は LLM の hallucination への応用．↩︎

  20. 「筆者は，conformal prediction などの post-hoc な手法は，便利かも知れないが，「信頼区間」や「\(P\)-値」のような側面（第 2.3 節）も併せ持つのではないかと危惧しながら見ている．」と当初は書いていたが，どうもそう簡単な話ではないようである．(Papamarkou et al., 2024) を読んで思った．↩︎

  21. (Papamarkou et al., 2024, p. 5) 3.4節．↩︎

  22. (Wang et al., 2024) が最新のサーベイであるようだ．↩︎

  23. Philipp Hennig Probabilistic ML - Lecture 1 - Introduction “Statistical Learning Theory is about Bayesian Reasoning when you don’t say out aloud what the prior is.”↩︎

  24. これを 証拠 (model evidence) ともいう．↩︎

  25. 事前分布として非有限な測度を用いた場合など，例外もある．↩︎

  26. “most conventional optimization-based machine-learning approaches have probabilistic analogues that handle uncertainty in a more principled manner.” (Ghahramani, 2015, p. 458)．↩︎

  27. (Neal and Hinton, 1998) など．↩︎

  28. (Ghahramani, 2015, p. 458) はこれを モデルの属人化 (personalization of models) と呼んでいる．↩︎

  29. (Ghahramani, 2015, p. 453) “probabilistic programming offers an elegant way of generalizing graphical models, allowing a much richer representation of models.”．↩︎

  30. “More generally, Bayesian optimization is a special case of Bayesian numerical computation, which is re-emerging as a very active area of research, and includes topics such as solving ordinary differential equations and numerical integration.” (Ghahramani, 2015, p. 456)．↩︎

  31. “All commonly used lossless data compression algorithms (for example, gzip) can be viewed as probabilistic models of sequences of symbols.” (Ghahramani, 2015, p. 456)．↩︎

  32. (Steinruecken et al., 2015) は記号列に対するノンパラメトリックモデルを改良することで，データ圧縮アルゴリズム PPM を改良した良い例である．↩︎